Coursera 吴恩达机器学习 课程笔记
监督学习和无监督学习
监督学习
维基百科中的定义:
监督式学习(英语:Supervised learning),是一个机器学习中的方法,可以由训练资料中学到或建立一个模式(函数 / learning model),并依此模式推测新的实例。训练资料是由输入物件(通常是向量)和预期输出所组成。函数的输出可以是一个连续的值(称为回归分析),或是预测一个分类标签(称作分类)
在监督学习中, 我们的预测结果可以是连续值, 也可以是离散值. 我们根据这样的属性将监督学习氛围回归问题和分类问题.
监督学习举例
回归问题
通过给定的一个房子的面积来预测这个房子在市场中的价格. 这里的房子的面积就是特征, 房子的价格就是一个输出值. 为了解决这个问题, 我们获取了大量的房地产数据, 每一条数据都包含房子的面积及其对应价格. 第一, 我们的数据不仅包含房屋的面积, 还包含其对应的价格, 而我们的目标就是通过面积预测房价. 所以这应该是一个监督学习; 其次, 我们的输出数据房价可以看做是连续的值, 所以这个问题是一个回归问题.
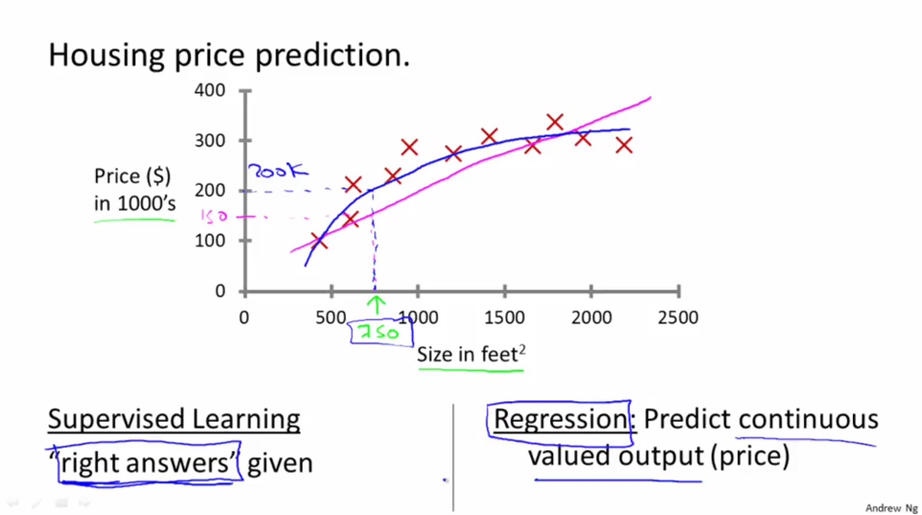
分类问题
我们的目标应该是要对数据进行分类. 现在我们的数据是有关乳腺癌的医学数据, 它包含了肿瘤的大小以及该肿瘤是良性的还是恶性的. 我们的目标是给定一个肿瘤的大小来预测它是良性还是恶性. 我们可以用0代表良性,1代表恶性. 这就是一个分类问题, 因为我们要预测的是一个离散值.
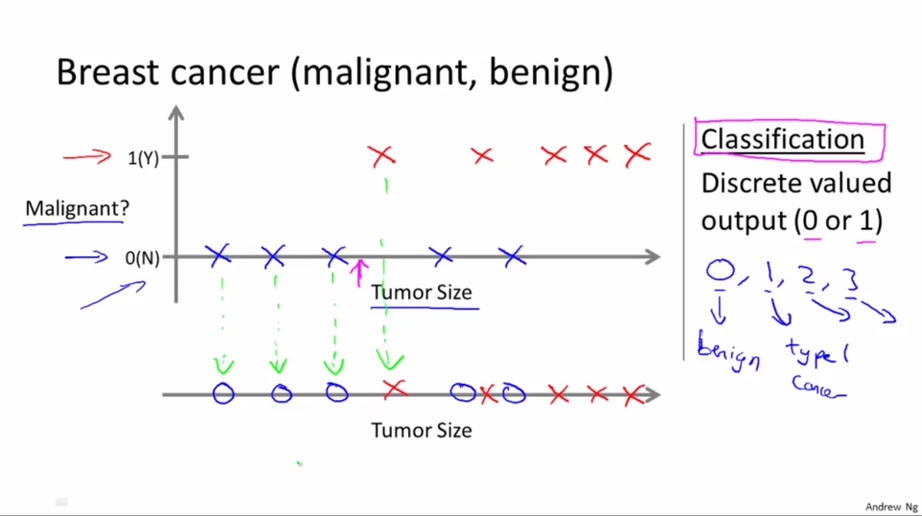
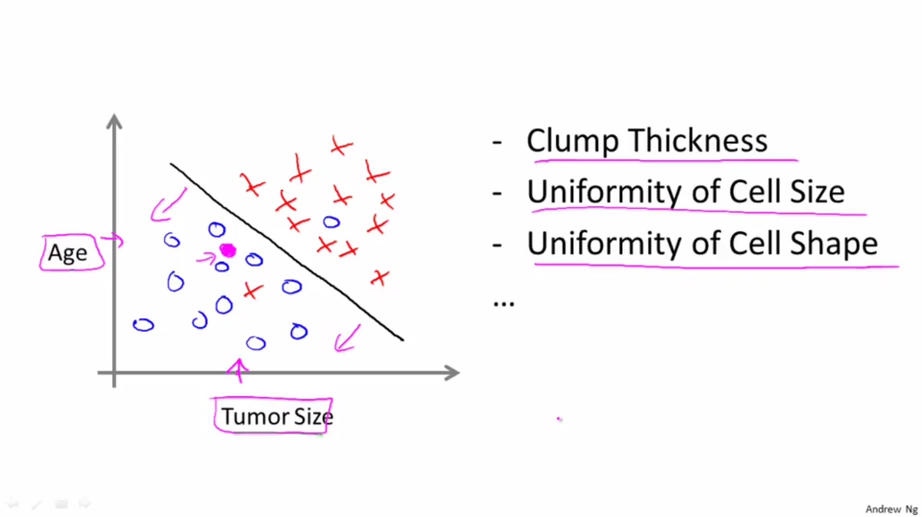
在这个例子中特征只有一个即瘤的大小。 对于大多数机器学习的问题, 特征往往有多个(上面的房价问题也是, 实际中特征不止是房子的面积). 例如下图, 有“年龄”和“肿瘤大小”两个特征。
无监督学习
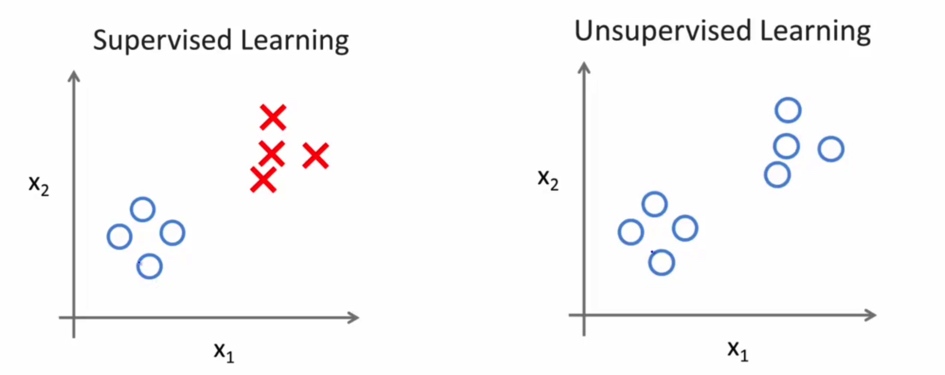
在无监督学习中, 我们的数据并没有给出特定的标签, 例如上面例子中的房价或者是良性还是恶性. 我们目标也从预测某个值或者某个分类变成了寻找数据集中特殊的或者对我们来说有价值结构.
无监督学习举例
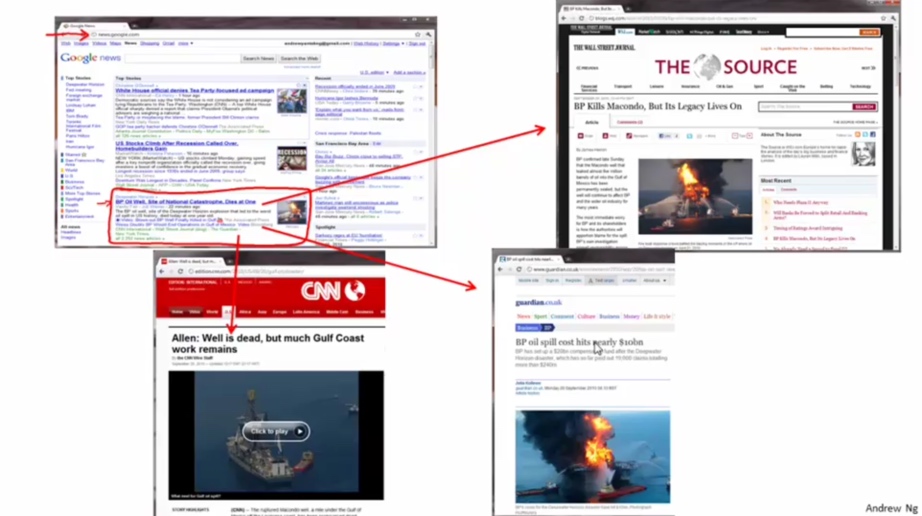
新闻分类
Google News搜集网上的新闻,并且根据新闻的主题将新闻分成许多簇, 然后将在同一个簇的新闻放在一起。如图中红圈部分都是关于BP Oil Well各种新闻的链接,当打开各个新闻链接的时候,展现的都是关于BP Oil Well的新闻。
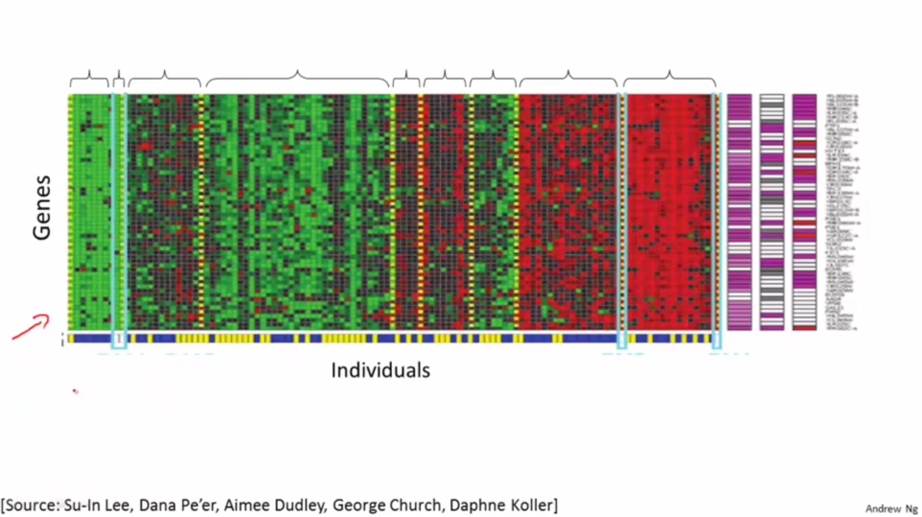
根据给定基因将人群分类
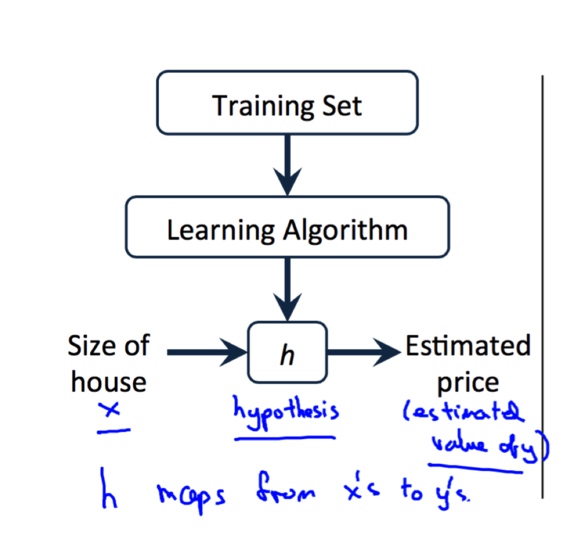
单变量线性回归
基本概念
训练集
由训练样例(training example)组成的集合就是训练集(training set)
假设函数
使用某种学习算法对训练集的数据进行训练, 我们可以得到假设函数(Hypothesis Function)
我们使用如下方法表示假设函数,
$$ {h_\theta(x)=\theta_0+\theta_1x} $$
以上这个模型就叫做单变量的线性回归(Linear Regression with One Variable).
代价函数
什么是代价函数
只要我们知道了假设函数, 我们就可以进行预测了. 关键是, 假设函数中有两个未知的量$\theta_0$,$\theta_1$. 当选择不同的$\theta_0$和$\theta_1$时, 我们模型的效果肯定是不一样的. 我们的想法是选择某个$\theta_0$和$\theta_1$,使得对于训练样例$(x,y)$,$h_\theta(x)$最“接近”$y$。越是接近, 代表这个假设函数越是准确, 这里我们选择均方误差来作为衡量标准, 即我们想要每个样例的估计值与真实值之间差的平方的均值最小:(其中$1/2$只是为了我们后面计算方便)
$$
{\mathop{min}\limits_{\theta_0,\theta_1}\frac{1}{2m}\sum_{i=0}^m\left(h_\theta(x^{(i)})-y^{(i)}\right)^2}
$$
记作:
$${J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=0}^m\left(h_\theta(x^{(i)})-y^{(i)}\right)^2 }$$
这样就得到了我们的代价函数(cost function), 也就是我们的优化目标, 我们想要代价函数最小:
$$ \mathop{min}\limits_{\theta_0,\theta_1}J(\theta_0,\theta_1)$$
代价函数和假设函数
对于不同的$\theta_1$,对应着不同的假设函数$h_\theta(x)$,于是就有了不同的代价函数$J (\theta_1)$的值。将这些点连接起来就可以得到$J(\theta_1)$和$\theta_1$关系的图像:
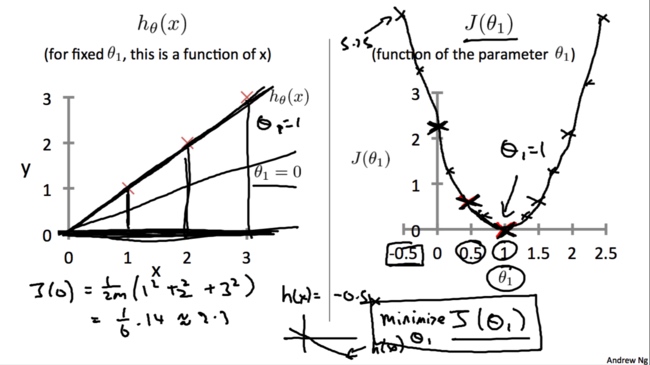
我们的目标是找到一个$\theta$使得$J(\theta_1)$最小
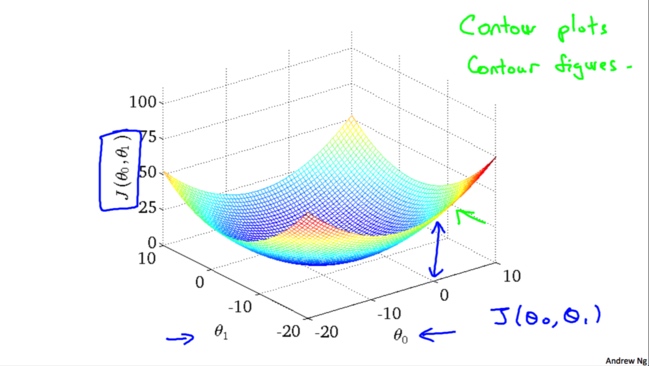
如果我们考虑两个变量,能够绘制$J(\theta_0,\theta_1)$的图形如下
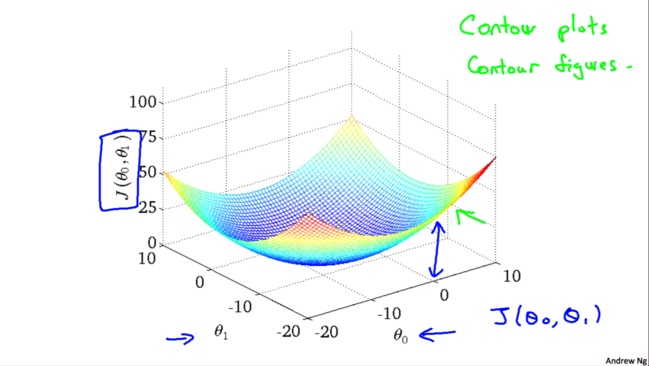
由于3D图形不太方便我们研究,我们就使用二维的等高线(上图右上角教授写的contour plots/figures),这样看上去比较清楚一些。越靠近中心表示$J(\theta_0,\theta_1)$值越小
梯度下降算法
梯度下降
梯度下降算法是一种优化算法, 它可以帮助我们找到一个函数的局部极小值点. 它不仅仅可以用在线性回归模型中, 在机器学习许多其他的模型中也可以使用它. 对于我们现在研究的单变量线性回归来说, 我们想要使用梯度下降来找到最优的$\theta_0$,$\theta_1$。
它的思想是,首先随机选择两个$\theta_0$,$\theta_1$,不断改变他们的值使得$J(\theta)$最小,最终找到$J(\theta)$的最小点
可以把梯度下降的过程想象成下山坡, 如果想要尽可能快的下坡, 应该每次都往坡度最大的方向下山.
算法过程:(要注意的是,算法是每次同时改变$\theta_0$和$\theta_1$的值)

梯度和学习率
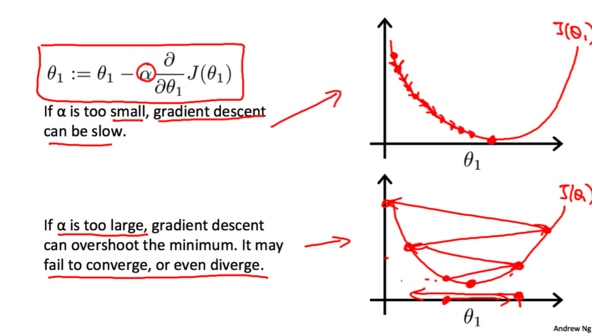
学习率$\alpha$会影响梯度下降的幅度。如果$\alpha$的值太小,$\theta$的值每次会变化很小,那么梯度下降就会比较慢;相反,如果$\alpha$过大,$\theta$的值每次就会变化很大,有可能超过最低点,可能导致永远没法到达最低点。
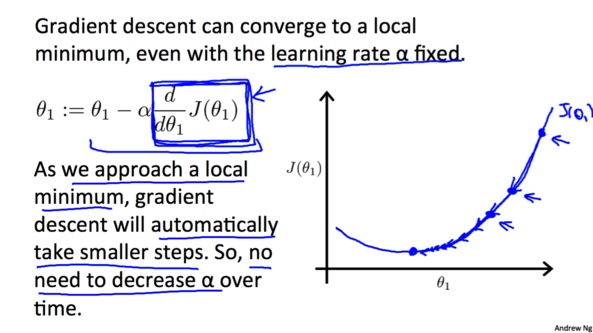
由于随着越来越接近最低点, 相应的梯度(绝对值)也会逐渐减小,所以每次下降程度就会越来越小, 我们并不需要减小$\alpha$的值来减小下降程度。
计算梯度
将偏导计算出来就得到了完整梯度下降算法:

事实上,用于线性回归的代价函数总是一个凸函数(Convex Function)。这样的函数没有局部最优解,只有一个全局最优解。所以我们在使用梯度下降的时候,总会得到一个全局最优解。
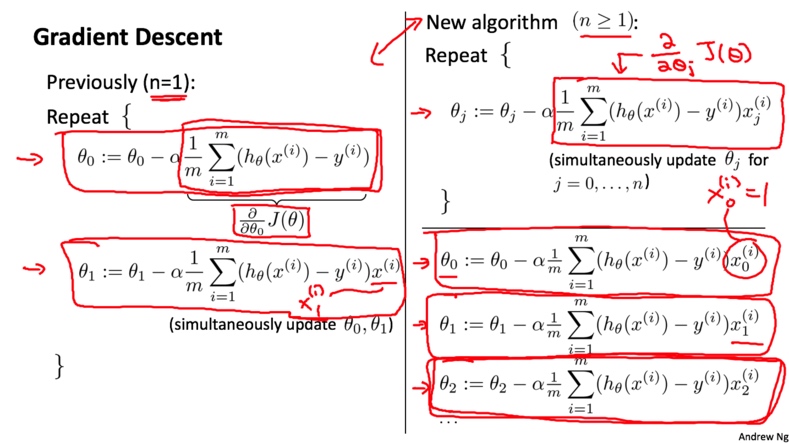
多变量线性回归
假设函数
在之前的单变量线性回归中, 我们的问题只涉及到了房子面积这一个特征。在实际问题中, 会有很多特征. 例如, 除了房子面积, 还有房子的卧室数量, 房子的楼层数, 房子建筑年龄.
在单变量线性回归中假设函数为:
$${h_\theta(x)=\theta_0+\theta_1x}$$
现在对于多变量,可以设其假设函数为:
$${h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n}$$

得到其向量表示:
$${h_\theta(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n= \theta^Tx}$$
梯度下降
多变量情况下的梯度下降其实没有区别, 只需要把对应的偏导数项换掉即可
特征处理
特征缩放
如果每个特征的范围相差的很大, 梯度下降会很慢. 为了解决这个问题, 我们在梯度下降之前应该对数据做特征归缩放(Feature Scaling)处理, 从而将所有的特征的数量级都在一个差不多的范围之内, 以加快梯度下降的速度.
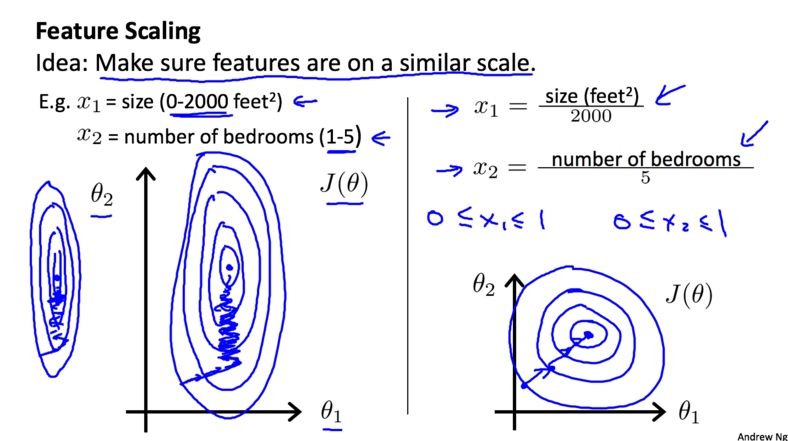
通常我们需要把特征都缩放到$[-1,1]$(附近)这个范围

均值均一化
还有一个特征处理的方法就是均值归一化(Mean normalization)
$${x_i=\frac{x_i-\mu_i}{max-min}}$$
代价函数与学习率
我们可以通过画出$\mathop{min}\limits_{\theta}J(\theta)$与迭代次数的关系来观察梯度下降的运行情况,
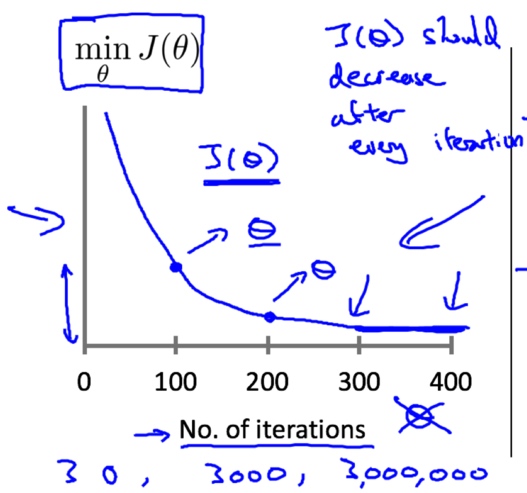
出现下面两种情况,应该选择更小的学习率$\alpha$,
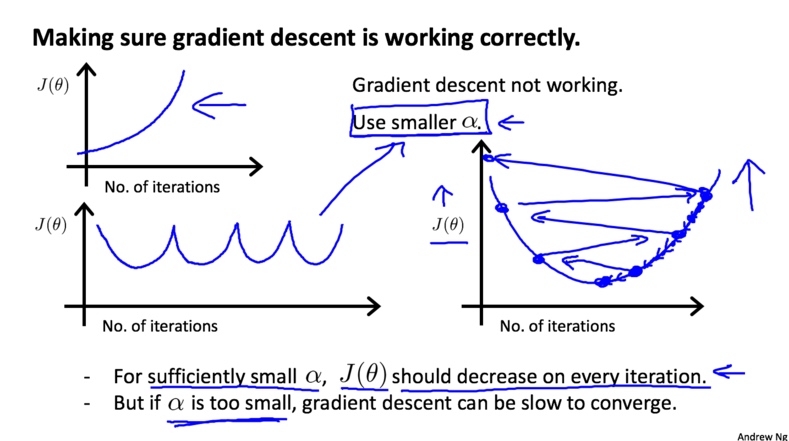
注意:
- 如果$\alpha$足够小,,那么$J(\theta)$在每次迭代之后都会减小
- 如果$\alpha$太小, 梯度下降会进行的非常缓慢.
进行尝试的值:
多项式回归
多项式回归(Polynomial Regression)是研究一个因变量与一个或多个自变量间多项式的回归分析方法。如果自变量只有一个时,称为一元多项式回归;如果自变量有多个时,称为多元多项式回归。
我们可以将房屋的面积作为第一个特征, 面积的平方作为第二个特征, 面积的立方作为第三个特征:
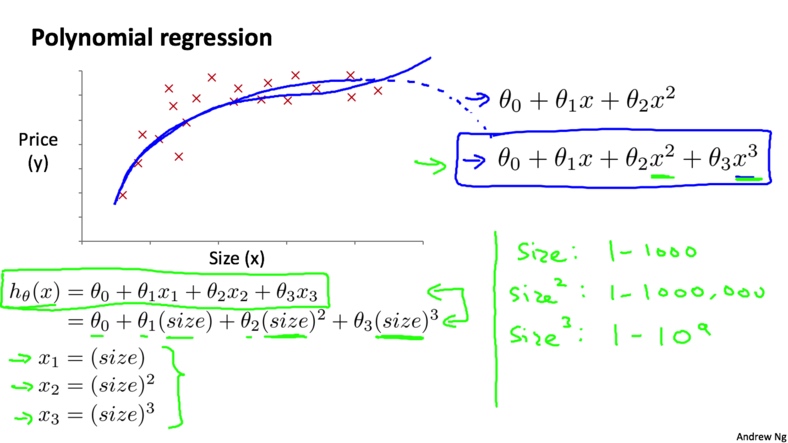
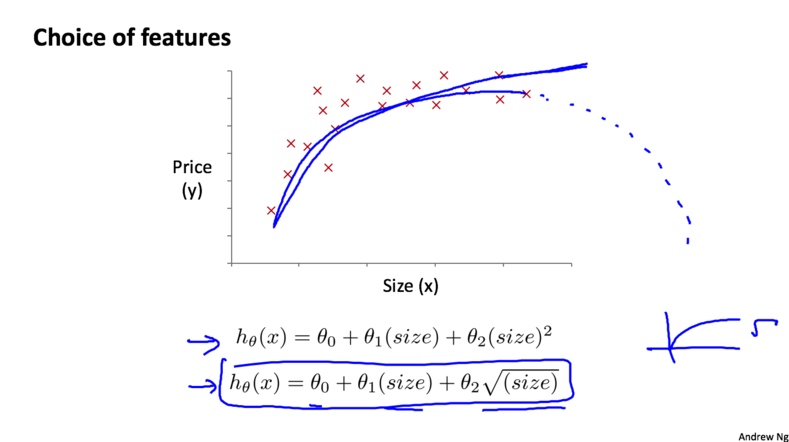
除了三次函数模型, 这里也可以选择平方根函数模型, 如下图所示
正规方程
正规方程介绍
之前我们一直是用的梯度下降求解最优值. 它的缺点就是需要进行很多次迭代才能得到全局最优解. 有没有更好的方法呢? 我们先来看一个最简单的例子, 假设现在的代价函数为$J(\theta)=a\theta^2+b\theta+c$,在导数等于0的时候取到最优解。

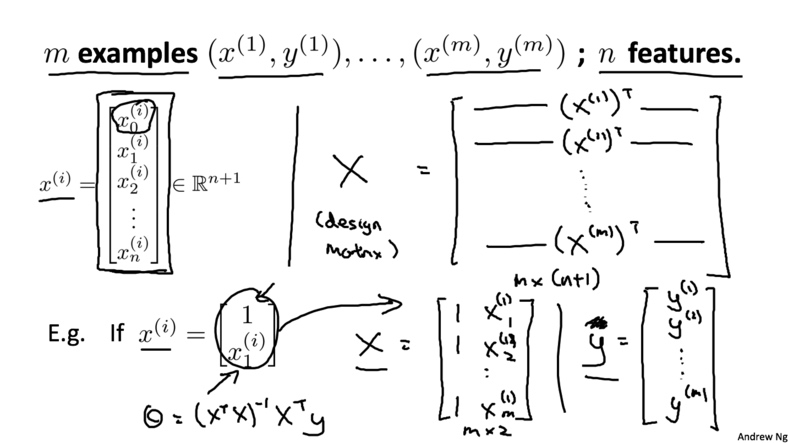
下面我们介绍一种向量化的求解方法。首先, 在数据集前加上一列$X_0$,值都为1,然后将所有的变量都放入矩阵$X$中(包括加上的$x_0$);再将输出值放入向量$y$中. 最后通过公式$$\theta=(X^TX)^{-1}X^Ty$$就可以算出最优解
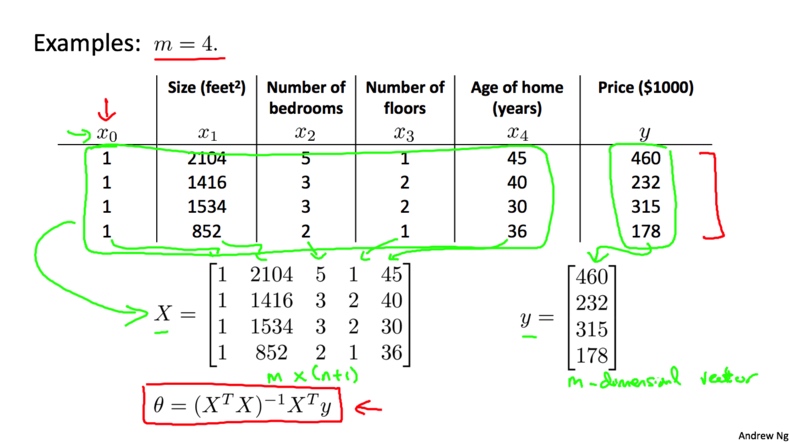
更通用的表达方式
梯度下降和正规方程的比较

正规方程不可逆的情况
使用正规方程还有一个问题就是$X^TX$可能存在不可逆的情况. 这个时候, 可能是因为我们使用了冗余的特征, 还有一个原因是我们使用了太多的特征(特征的数量超过了样本的数量). 对于这种情况我们可以删掉一些特征或者使用正则化(正则化在后面的课中讲).


